新二乘法(最小三乘法)

网站首页      最小二乘法      最小二乘法和最小三乘法比较

主题词：数据回归、多维、非线性、模型、应用

摘要：“新二乘法”是“最小二乘法”的改进法，它在数据回归计算时，不只计算模型的常数和系数，还计算模型中变量的幂值，使得非线性数据回归计算更简单结果更准确。

一、前言

“最小二乘法”在非线性数据回归时，要对模型进行数学替代和转换，回归结果也不是很准确。针对这些问题，我们对“最小二乘法”进行了改进，称之为“新二乘法”。

二、“新二乘法”原理

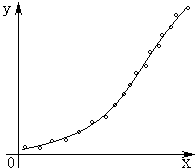
当研究两个变量  之间的相互关系时 ，实测得到一系列成对数据， 将这些数据描绘在x - y直角座标系中,可得到(图1)所示散点图，观察散点在一条曲线附近，设这条曲线的拟合方程(式1)为：

 图1

                   式1

式中： 是任意实数

为建立拟合方程，就要确定 值，用实测值 减计算值，即。

在计算的平方和如(式2)。

                          式2

把(式1)代入(式2)中，如式 3：

                式3

用函数分别对 求偏导数，令这三个偏导数等于零即：

            式4

                                            式5  

     式6  

推导发现方程组无解析解，利用计算机程序，对方程组做数值解，可以得出 和相关系数，相关系数越趋近于 1 ，模型拟合越好。

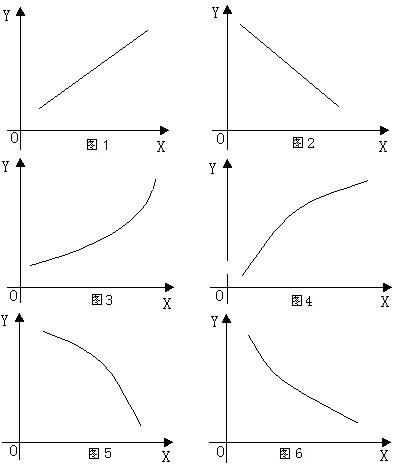
模型选择

一、机理研究法 

1.  机理研究法是研究某过程的内在联系，对过程假设后，而建立的两个或两个以上因素之间关系的数学方程式；对数学方程式做数学变形处理，找出与预设模型(数学方程式)相对应的元和目标函数，在利用数据回归计算机理模型的系数。 

  2.  机理研究法适合：采集数据的量少，数据的精度低，需用机理模型弥补这些不足。

二、数据研究法 

1.   数据研究法是对两维数据，以两维数据分别为目标函数和因素，因素 X 的变化引起目标函数 Y 变化，这种变化可分为六种情况如(图1)—(图6)。 

2. 第一种 线性增加，随因素 X 增加，因素 Y 匀速增大。 
   第二种 线性减少，随因素 X 增加，因素 Y 匀速减小。 
   第三种 非线性增加，随因素 X 增加，因素 Y 加速增大。 
   第四种 非线性增加，随因素 X 增加，因素 Y 减速增大。 
   第五种 非线性减少，随因素 X 增加，因素 Y 加速减小。
   第六种 非线性减少，随因素 X 增加，因素 Y 减速减小。 

3.  假设此六种情况方程式为（式1）： 
                                       式1

   第一种情况显然 a₀ > 0 时，a₁ ＞ 0、k ＝ 1 
   第二种情况显然 a₀ > 0 时，a₁ ＜ 0、k ＝ 1
   第三种情况显然 a₀ > 0 时，a₁ ＞ 0、k ＞ 1、k ＜ 0 
   第四种情况显然 a₀ > 0 时，a₁ ＞ 0、0 ＜ k ＜ 1 
   第五种情况显然 a₀ > 0 时，a₁ ＜ 0、0 ＜ k ＜ 1 
   第六种情况显然 a₀ > 0 时，a₁ ＜ 0、k ＞ 1、 k ＜ 0

4.  通过上述分析总结，确定回归参数(即每一元)的数学式，第三、六种情况，曲线上凹，与指数曲线相似，可选指数形式 e^X ； 第四、五种情况，曲线上凸，与对数形式相似，可选对数形式 LOG(X)(对数底为e)；若选择幂形式 X^k，可根据上述第一种情况至第六种情况中 a₀、a₁、a₂ 和 k 之间的关系选择 k 值。

  5.  数据研究法适合：采集数据较多，数据的精度较高。

三、选择回归参数注意问题 

  1.  当一因素数据中有 0 值时， 此因素数据不可作除数和取对数；可把此维数据加上一个数，使它大于零。
  2.  当一因素数据中有负数都有时，此因素数据不可做回归计算；可把此维数据乘上一个负数，使它大于零。
  3.  某因素数据取幂时，不可太大和太小，否则回归计算机会中断溢出；有时回归出的模型，不能逆运算。