|
Comparison “New Square Method” and “Least Square Method”
If Equation 1 as shown below is adopted to fit any data:
 Equation 1 Equation 1
The Comparison Table
between the “New Square Method”
and the “Least Square
Method”:
|
|
Least Square Method
|
New Square Method
|
|
Fitted Equations:
|
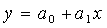
|

|
|
Calculated Regression
Results:
|
a0 and a1
|
a0, a1 and k
|
1. In the “new
square method”, the power value of the dependent variable is
calculated, while in the “least square method”, of the dependent variable is
calculated, while in the “least square method”,  is assumed to be 1. With the
calculated power value for the dependent variable, the new square method is
able to have the fitted equation generate a fitted line at any curve to
better fit the non-linear data. is assumed to be 1. With the
calculated power value for the dependent variable, the new square method is
able to have the fitted equation generate a fitted line at any curve to
better fit the non-linear data.
2.In the “new square method”, non-linear data with one factor can be regressed by applying the
following Equation 2 in the computer programs to obtain more accurate
fittings of non-linear data by regression models. can be regressed by applying the
following Equation 2 in the computer programs to obtain more accurate
fittings of non-linear data by regression models.
 Equation 2 Equation 2
In Equation 2:
 —
Variable. —
Variable.
 —
Function. —
Function.
 —Dimensional (two-dimensional). —Dimensional (two-dimensional).
 —
Element. —
Element.
 —
Constant. —
Constant.
 —
Coefficient. —
Coefficient.
 —
Power. —
Power.
3.As for the regression of non-linear data with multi-factors in the
“new square method”, the following Equation 3 can be utilized in computer
programs for this purpose. This equation takes into account both the
contribution of factors to the objective
function ( to the objective
function ( ) and the interplays among factors ) and the interplays among factors during the regression calculation, that is why the fitted
models are of high correlation. during the regression calculation, that is why the fitted
models are of high correlation.
 Equation 3
Equation 3
In Equation 3:
 —
Variable. —
Variable.
 —
Function. —
Function.
 — Dimensional (three-dimensional). — Dimensional (three-dimensional).
 —
Element. —
Element.
 —
Constant. —
Constant.
 —
Coefficient. —
Coefficient.
 —
Power. —
Power.
Note: Equation 9, which takes three-dimensional data as its
example, can be applied for the regression of data in curved surface data.
|