动态局部分析

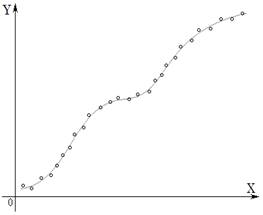
关键词：大数据，回归，算法，动态，局部，精准

摘要：“动态局部分析”是相关大数据建立数学模型的一种算法，它是在大数据中找和样品距离最近的局部样本，用局部样本建模，解决了大数据建模置信度低的问题，提高了模型计算精度。

一、前言

随着信息技术的发展，长期采集事物过程的数据，使得存储的数据范围变大，密度增高，变化越来越复杂，因而把这类数据称为大数据。假如这些数据是两维，把它描绘在平面直角坐标系中(如图 1)，显然数学关系式很难对它精准的拟合，为了解决这个问题，我们研发了“动态局部分析”。

图 1

二、动态局部分析

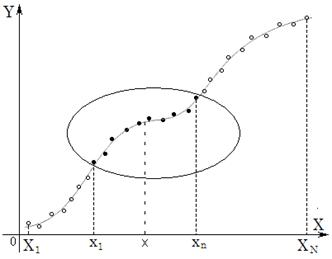
1. 对存储的大数据，通过画图比较，是否离群，是否符合实际规律等，剔除不合理的样本，用筛选后的样本，建立一个标准样本群，放在计算程序中，即 N 组样本(X₁，Y₁，X₂，Y₂ ，…… X_I，Y_I ，…… X_N，Y_N) ，令这N组样本为 A集合，其中I是样本序号，如图2 中全部点。

2. 每当有样品要通过 x 计算 y 时，用 x 值逐一和 A 集合中的 X_I 比较，找出和样品距离最近的 n 组样本 (x₁，y₁，x₂，y₂ ，…… x_i，y_i ，…… x_n，y_n) ，把这 n 组样本叫 B 集合，其中 i 是样本序号，n 值根据实际情况设定，如图 2 圆圈中实心数据点 。

显然 B 是 A 的子集合即

式 1

图 2

3. 图 2 圆圈中实心点， 是距离样品最近的样本 B 集合数据，它是 A 集合的局部，且较 A 集合曲线变化简单，因此，用 “新二乘法”对 B 集合样本回归建模，模型的置信度将有很大的提高，把 x 代入模型计算 y 更准确 。

4. 图 2 中圆圈外的空心点，距离样品远，对样品的影响小，可以忽略不计。

三. 结论

1. 不同的样品在计算 y 时，采用的建模数据不同，所以模型是动态变化的。

2．建模使用的样本是全部样本的一部分，所以是局部的。

3. 回归建模使用的局部样本，较全部样本曲线变化简单，使模型的置信度提高，所以计算的结果更准确。