Dynamic Local Analysis

Abstract: “Dynamic Local Analysis” is an algorithm to establish mathematic model with the big data. On the basis of its features to search for the local samples closest to the specimen and to establish models with local samples, the problem of low confidence level of big data modeling is solved, and the model calculation accuracy is increased.

1. Preface

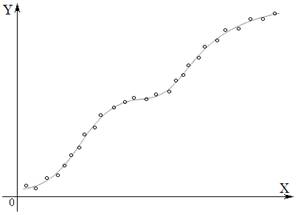
With the development of information technology, long-time data acquisition of the process of things results in the increasing of dimensions, the largening of scope, the rising of density, and more complex changes of the stored data which is called the big data accordingly. Provided that the data is two-dimensional and is put into a rectangular coordinate system (as shown in Fig. 1), it is obvious that to find a mathematic model as an accurate fit is of great difficulty. To solve this problem, we develop the method called "Dynamic Local Analysis”.

Fig. 1

2. Dynamic Local Analysis

2.1 The stored big data are compared through illustration to distinguish outliners and the compliance of regular patterns. The unreasonable samples are eliminated, and the screened samples are used to establish a standard sample group(x₁，y₁，x₂，y₂ ，…… x_i，y_i ，…… x_m，y_m, m is the sample size, as all data points shown in Fig. 2.

2.2. When the specimen is to calculate y via x, the x value is to be compared with x_i in the standard sample group in sequence to find out m sets of local samples (x₁，y₁，x₂，y₂ ，…… x_i，y_i ，…… x_n，y_n) , which are the closest to the specimen, n is set according to actual conditions, as solid core data points shown in Fig. 2; n sets of local samples are used to establish model to calculate the y value.

2.3. The hollow points out of the circle in Fig. 2 are remote from the specimen and have very little influence which can be ignored from the calculation.

Fig. 2

3. Conclusion

3.1. When y is calculated with the different specimen, the data to establish model is different; as a result, the models change dynamically.

3.2. The samples used for modeling are part of all samples, so it is thus local.

3.3. The local samples used for regression modeling are simpler in curve variation compared to the whole of samples; therefore, the confidence level of modeling is increased and the accuracy of calculated results is improved.